A monomial contains one term, a binomial contains two terms, and a polynomial contains more than two terms. Linear expressions have no exponents. A quadratic expression contains variables that are squared (raised to the exponent of 2).
Navy YN Yeoman ASVAB Study Guide
| Branch | Navy |
| MOS | YN |
| Title | Yeoman |
| Description | Enforces the regulations and orders relative to the protection and security of vessels, harbors, ports, and waterfront facilities; supervises and controls the safe handling, transportation, stowage, and storage of explosives and other dangerous cargoes; in restricted areas, prevents unauthorized persons from entering upon the vessel or waterfront facility, carefully examines all authorized persons. Performs general police patrol duty; arrests persons and collects evidence; controls access to restricted areas; conducts surveillance of vessels and identifies offenses; inspects vessels, cargo, and waterfront facilities; inspects documentation; conducts vessel searches. Able to perform the duties required for E3 through E6; plans and conducts training programs; supervises cargo transfers and inspection procedures; cooperates with private cleanup contractors; plans, implements, and monitors security of vessels, harbors, and ports; coordinates security for facilities, responds to security threats, conducts threat assessment, supervises officers during operations, assesses computerized databases to verify information, provides mentoring for junior officers; serves as safety officer; supervises and directs law enforcement procedures, explosives-loading detail, and the loading, stowing, security, and offloading of dangerous cargo; supervises officers in the field of operations, plans for training needs, scheduling, debrief, evaluates and generates reports from operations, assures accuracy of intelligence information; serves as senior enlisted technical or specialty administrator; manages and supervises operations and procedures involving security and law enforcement, dangerous cargo, and safety and fire prevention; develops training and safety programs; establishes objectives and sets priorities; performs operational administrative functions; prepares correspondence concerning fiscal, supply, and administrative matters; assists in the formulation of plans, policies, and budget requirements; may supplement the officer corps in the overall supervision and administration of personnel and equipment; may also supervise personnel in other specialty areas. Able to perform the duties required for E3 and E4; conducts investigations and interviews; conducts vessel searches using electronic survey equipment; supervises training and development of subordinate personnel; writes investigative reports; instructs subordinate personnel in procedures for manning a security zone, use of service pistol and safety requirements for explosives; serves as liaison with other law enforcement agencies; completes permit applications for explosives and other dangerous cargo; supervises use of loading equipment to determine safe operation; conducts facilities inspections. |
| Subtests | Math Knowledge, Paragraph Comprehension, Word Knowledge |
Math Knowledge
- 28 Questions
- 38 Problems
- 55 Flash Cards
Algebra
Expressions 4 9 8
Classifications
Operations Involving Monomials
You can only add or subtract monomials that have the same variable and the same exponent. However, you can multiply and divide monomials with unlike terms.
Multiplying Binomials
To multiply binomials, use the FOIL method. FOIL stands for First, Outside, Inside, Last and refers to the position of each term in the parentheses.
Factoring Quadratics
To factor a quadratic expression, apply the FOIL (First, Outside, Inside, Last) method in reverse.
Solving Equations 2 9 2
One Variable
An equation is two expressions separated by an equal sign. The key to solving equations is to repeatedly do the same thing to both sides of the equation until the variable is isolated on one side of the equal sign and the answer on the other.
Two Variables
When solving an equation with two variables, replace the variables with the values given and then solve the now variable-free equation. (Remember order of operations, PEMDAS, Parentheses, Exponents, Multiplication/Division, Addition/Subtraction.)
Two Equations
When presented with two equations with two variables, evaluate the first equation in terms of the variable you're not solving for then insert that value into the second equation. For example, if you have x and y as variables and you're solving for x, evaluate one equation in terms of y and insert that value into the second equation then solve it for x.
Quadratic Equations
When solving quadratic equations, if the equation is not set equal to zero, first manipulate the equation so that it is set equal to zero: ax2 + bx + c = 0. Then, factor the quadratic and, because it's set to zero, you know that one of the factors must equal zero for the equation to equal zero. Finding the value that will make each factor, i.e. (x + ?), equal to zero will give you the possible value(s) of x.
Inequalities
Solving equations with an inequality (<, >) uses the same process as solving equations with an equal sign. Isolate the variable that you're solving for on one wide of the equation and put everything else on the other side. The only difference is that your answer will be expressed as an inequality (x > 5) and not as an equality (x = 5).
Geometry
Lines & Angles 5 2 14
Line Segment
A line segment is a portion of a line with a measurable length. The midpoint of a line segment is the point exactly halfway between the endpoints. The midpoint bisects (cuts in half) the line segment.
Right Angle

A right angle measures 90 degrees and is the intersection of two perpendicular lines. In diagrams, a right angle is indicated by a small box completing a square with the perpendicular lines.
Acute & Obtuse Angles
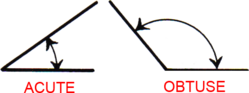
An acute angle measures less than 90°. An obtuse angle measures more than 90°.
Angles Around Lines & Points
Angles around a line add up to 180°. Angles around a point add up to 360°. When two lines intersect, adjacent angles are supplementary (they add up to 180°) and angles across from either other are vertical (they're equal).
Parallel Lines
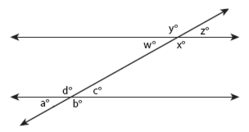
Parallel lines are lines that share the same slope (steepness) and therefore never intersect. A transversal occurs when a set of parallel lines are crossed by another line. All of the angles formed by a transversal are called interior angles and angles in the same position on different parallel lines equal each other (a° = w°, b° = x°, c° = z°, d° = y°) and are called corresponding angles. Alternate interior angles are equal (a° = z°, b° = y°, c° = w°, d° = x°) and all acute angles (a° = c° = w° = z°) and all obtuse angles (b° = d° = x° = y°) equal each other. Same-side interior angles are supplementary and add up to 180° (e.g. a° + d° = 180°, d° + c° = 180°).
Polygons 8 10 16
Triangle Geometry
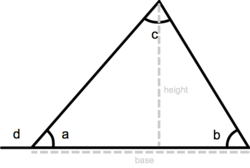
A triangle is a three-sided polygon. It has three interior angles that add up to 180° (a + b + c = 180°). An exterior angle of a triangle is equal to the sum of the two interior angles that are opposite (d = b + c). The perimeter of a triangle is equal to the sum of the lengths of its three sides, the height of a triangle is equal to the length from the base to the opposite vertex (angle) and the area equals one-half triangle base x height: a = ½ base x height.
Triangle Classification
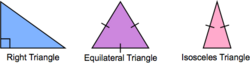
An isosceles triangle has two sides of equal length. An equilateral triangle has three sides of equal length. In a right triangle, two sides meet at a right angle.
Pythagorean Theorem
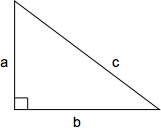
The Pythagorean theorem defines the relationship between the side lengths of a right triangle. The length of the hypotenuse squared (c2) is equal to the sum of the two perpendicular sides squared (a2 + b2): c2 = a2 + b2 or, solved for c, \(c = \sqrt{a + b}\)
Quadrilateral
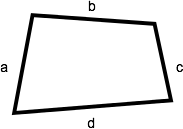
A quadrilateral is a shape with four sides. The perimeter of a quadrilateral is the sum of the lengths of its four sides (a + b + c + d).
Rectangle & Square
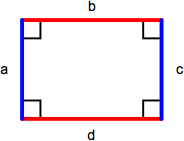
A rectangle is a parallelogram containing four right angles. Opposite sides (a = c, b = d) are equal and the perimeter is the sum of the lengths of all sides (a + b + c + d) or, comonly, 2 x length x width. The area of a rectangle is length x width. A square is a rectangle with four equal length sides. The perimeter of a square is 4 x length of one side (4s) and the area is the length of one side squared (s2).
Parallelogram
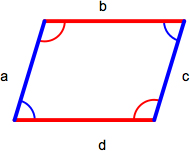
A parallelogram is a quadrilateral with two sets of parallel sides. Opposite sides (a = c, b = d) and angles (red = red, blue = blue) are equal. The area of a parallelogram is base x height and the perimeter is the sum of the lengths of all sides (a + b + c + d).
Rhombus
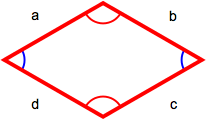
A rhombus has four equal-length sides with opposite sides parallel to each other. The perimiter is the sum of the lengths of all sides (a + b + c + d) or, because all sides are the same length, 4 x length of one side (4s).
Trapezoid
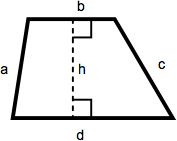
A trapezoid is a quadrilateral with one set of parallel sides. The area of a trapezoid is one-half the sum of the lengths of the parallel sides multiplied by the height. In this diagram, that becomes ½(b + d)(h).
Circles 5 2 8
Dimensions
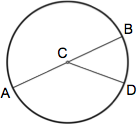
A circle is a figure in which each point around its perimeter is an equal distance from the center. The radius of a circle is the distance between the center and any point along its perimeter (AC, CB, CD). A chord is a line segment that connects any two points along its perimeter (AB, AD, BD). The diameter of a circle is the length of a chord that passes through the center of the circle (AB) and equals twice the circle's radius (2r).
Calculations
The circumference of a circle is the distance around its perimeter and equals π (approx. 3.14159) x diameter: c = π d. The area of a circle is π x (radius)2 : a = π r2.
Solids 2 4 5
Cubes
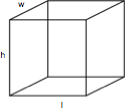
A cube is a rectangular solid box with a height (h), length (l), and width (w). The volume is h x l x w and the surface area is 2lw x 2wh + 2lh.
Cylinders
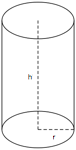
A cylinder is a solid figure with straight parallel sides and a circular or oval cross section with a radius (r) and a height (h). The volume of a cylinder is π r2h and the surface area is 2(π r2) + 2π rh.
Coordinate Geometry 2 2 2
Coordinate Grid
The coordinate grid is composed of a horizontal x-axis and a vertical y-axis. The center of the grid, where the x-axis and y-axis meet, is called the origin.
Slope-Intercept Equation
A line on the coordinate grid can be defined by a slope-intercept equation: y = mx + b. For a given value of x, the value of y can be determined given the slope (m) and y-intercept (b) of the line. The slope of a line is change in y over change in x, \({\Delta y \over \Delta x}\), and the y-intercept is the y-coordinate where the line crosses the vertical y-axis.