Mechanics deals with motion and the forces that produce motion.
ASVAB Mechanical Comprehension Study Guide
| Branch | All |
| Description | |
| Subtests | Mechanical Comprehension |
Mechanical Comprehension
- 94 Questions
- 34 Problems
- 100 Flash Cards
Fundamentals of Mechanics
Principles 10 1 11
Mechanics
Mass
Mass is a measure of the amount of matter in an object. In general, larger objects have larger mass than smaller objects but mass ultimately depends on how compact (dense) a substance is.
Inertia
The more mass a substance has the more force is required to move it or to change its direction. This resistance to changes in direction is known as inertia.
Net Force
In mechanics, multiple forces are often acting on a particular object and, taken together, produce the net force acting on that object. Like force, net force is a vector quantity in that it has magnitude and direction.
Newton's Second Law of Motion
Newton's Second Law of Motion states that "The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object." This Law describes the linear relationship between mass and acceleration when it comes to force and leads to the formula F = ma or force equals mass multiplied by rate of acceleration.
Universal Gravitation
Newton's Law of Univeral Gravitation defines the general formula for the attraction of gravity between two objects: \(\vec{F_{g}} = { Gm_{1}m_{2} \over r^2}\) . In the specific case of an object falling toward Earth, the acceleration due to gravity (g) is approximately 9.8 m/s2.
Weight
Mass is an intrinsic property of matter and does not vary. Weight is the force exerted on the mass of an object due to gravity and a specific case of Newton's Second Law of Motion. Replace force with weight and acceleration with acceleration due to gravity on Earth (g) and the result is the formula for weight: W = mg or, substituting for g, weight equals mass multiplied by 9.8 m/s2.
Boyle's Law
Boyle's law states that "for a fixed amount of an ideal gas kept at a fixed temperature, pressure and volume are inversely proportional". Expressed as a formula, that's \(\frac{P_1}{P_2} = \frac{V_2}{V_1}\)
Friction 11 9
Kinetic Friction
Friction resists movement. Kinetic (also called sliding or dynamic) friction resists movement in a direction opposite to the movement. Because it opposes movement, kinetic friction will eventually bring an object to a stop. An example is a rock that's sliding across ice.
Static Friction
Static friction is friction between two or more solid objects that are not moving relative to each other. An example is the friction that prevents a box on a sloped surface from sliding farther down the surface.
Coefficient of Friction
Coefficient of friction (μ) represents how much two materials resist sliding across each other. Smooth surfaces like ice have low coefficients of friction while rough surfaces like concrete have high μ.
Normal Force
Normal force (FN) represents the force a surface exerts when an object presses against it.
Force of Friction
The formula for force of friction (Ff) is the same whether kinetic or static friction applies: Ff = μFN. To distinguish between kinetic and static friction, μk and μs are often used in place of μ.
Kinetic vs. Static Friction
For any given surface, the coefficient of static friction is higher than the coefficient of kinetic friction. More force is required to initally get an object moving than is required to keep it moving. Additionally, static friction only arises in response to an attempt to move an object (overcome the normal force between it and the surface).
Normal Force vs. Weight
Normal force arises on a flat horizontal surface in response to an object's weight pressing it down. Consequently, normal force is generally equal to the object's weight.
Other Forces 11 2 10
Drag
Drag is friction that opposes movement through a fluid like liquid or air. The amount of drag depends on the shape and speed of the object with slower objects experiencing less drag than faster objects and more aerodynamic objects experiencing less drag than those with a large leading surface area.
Tension
Tension is a force that stretches or elongates something. When a cable or rope is used to pull an object, for example, it stretches internally as it accepts the weight that it's moving. Although tension is often treated as applying equally to all parts of a material, it's greater at the places where the material is under the most stress.
Hydraulic Pressure
Hydraulics is the transmission of force through the use of liquids. Liquids are especially suited for transferring force in complex machines because they compress very little and can occupy very small spaces. Hydraulic pressure is calculated by dividing force by the area over which it is applied: P = F/A where F is force in pounds, A is area in square inches, and the resulting pressure is in pounds per square inch (psi).
Pascal's Law
Pascal's law states that a pressure change occurring anywhere in a confined incompressible fluid is transmitted throughout the fluid such that the same change occurs everywhere. For a hydraulic system, this means that a pressure applied to the input of the system will increase the pressure everywhere in the system.
Torque
Torque measures force applied during rotation: τ = rF. Torque (τ, the Greek letter tau) = the radius of the lever arm (r) multiplied by the force (F) applied. Radius is measured from the center of rotation or fulcrum to the point at which the perpendicular force is being applied. The resulting unit for torque is newton-meter (N-m) or foot-pound (ft-lb).
Principle of Moments
When a system is stable or balanced (equilibrium) all forces acting on the system cancel each other out. In the case of torque, equilibrium means that the sum of the anticlockwise moments about a center of rotation equal the sum of the clockwise moments.
Energy, Work, & Power 14 3 14
Joules
The Joule (J) is the standard unit of energy and has the unit \({kg \times m^2} \over s^2\).
Kinetic Energy
Kinetic energy is the energy of movement and is a function of the mass of an object and its speed: \(KE = {1 \over 2}mv^2\) where m is mass in kilograms, v is speed in meters per second, and KE is in joules. The most impactful quantity to kinetic energy is velocity as an increase in mass increases KE linearly while an increase in speed increases KE exponentially.
Potential Energy
Potential energy is the energy of an object by virtue of its position relative to other objects. It is energy that has the potential to be converted into kinetic energy.
Gravitational Potential Energy
Gravitational potential energy is energy by virtue of gravity. The higher an object is raised above a surface the greater the distance it must fall to reach that surface and the more velocity it will build as it falls. For gravitational potential energy, PE = mgh where m is mass (kilograms), h is height (meters), and g is acceleration due to gravity which is a constant (9.8 m/s2).
Conservation of Mechanical Energy
As an object falls, its potential energy is converted into kinetic energy. The principle of conservation of mechanical energy states that, as long as no other forces are applied, total mechanical energy (PE + KE) of the object will remain constant at all points in its descent.
Work
Work is accomplished when force is applied to an object: W = Fd where F is force in newtons (N) and d is distance in meters (m). Thus, the more force that must be applied to move an object, the more work is done and the farther an object is moved by exerting force, the more work is done.
Work-Energy Theorem
The work-energy theorem states that the work done by the sum of all forces acting on a particle equals the change in the kinetic energy of the particle. Simply put, work imparts kinetic energy to the matter upon which the work is being done.
Power
Power is the rate at which work is done, P = w/t, or work per unit time. The watt (W) is the unit for power and is equal to 1 joule (or newton-meter) per second. Horsepower (hp) is another familiar unit of power used primarily for rating internal combustion engines. A 1 hp machine does 550 ft⋅lb of work in 1 second and 1 hp equals 746 watts.
Machines
Simple Machines 28 26 33
Types of Simple Machines
The six types of simple machines are the lever, wheel and axle, pulley, inclined plane, wedge, and screw.
Mechanical Advantage
Mechanical advantage is a measure of the force amplification achieved by using a tool, mechanical device or machine system. Such a device utilizes input force and trades off forces against movement to amplify and/or change its direction.
Efficiency
The efficiency of a machine describes how much of the power put into the machine is turned into movement or force. A 100% efficient machine would turn all of the input power into output movement or force. However, no machine is 100% efficient due to friction, heat, wear and other imperfections that consume input power without delivering any output.
Inclined Plane

An inclined plane is a simple machine that reduces the force needed to raise an object to a certain height. Work equals force x distance and, by increasing the distance that the object travels, an inclined plane reduces the force necessary to raise it to a particular height. In this case, the mechanical advantage is to make the task easier. An example of an inclined plane is a ramp.
Wedge
The wedge is a moving inclined plane that is used to lift, hold, or break apart an object. A wedge converts force applied to its blunt end into force perpendicular to its inclined surface. In contrast to a stationary plane where force is applied to the object being moved, with a wedge the object is stationary and the force is being applied to the plane. Examples of a wedge include knives and chisels.
First-Class Lever

A first-class lever is used to increase force or distance while changing the direction of the force. The lever pivots on a fulcrum and, when a force is applied to the lever at one side of the fulcrum, the other end moves in the opposite direction. The position of the fulcrum also defines the mechanical advantage of the lever. If the fulcrum is closer to the force being applied, the load can be moved a greater distance at the expense of requiring a greater input force. If the fulcrum is closer to the load, less force is required but the force must be applied over a longer distance. An example of a first-class lever is a seesaw / teeter-totter.
Second-Class Lever
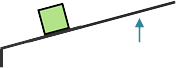
A second-class lever is used to increase force on an object in the same direction as the force is applied. This lever requires a smaller force to lift a larger load but the force must be applied over a greater distance. The fulcrum is placed at one end of the lever and mechanical advantage increases as the object being lifted is moved closer to the fulcrum or the length of the lever is increased. An example of a second-class lever is a wheelbarrow.
Third-Class Lever

A third-class lever is used to increase distance traveled by an object in the same direction as the force applied. The fulcrum is at one end of the lever, the object at the other, and the force is applied between them. This lever does not impart a mechanical advantage as the effort force must be greater than the load but does impart extra speed to the load. Examples of third-class levers are shovels and tweezers.
Fixed Pulley
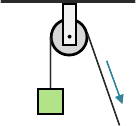
A fixed pulley is used to change the direction of a force and does not multiply the force applied. As such, it has a mechanical advantage of one. The benefit of a fixed pulley is that it can allow the force to be applied at a more convenient angle, for example, pulling downward or horizontally to lift an object instead of upward.
Block and Tackle
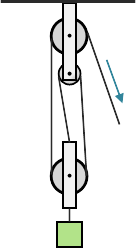
Two or more pulleys used together constitute a block and tackle which, unlike a fixed pulley, does impart mechanical advantage as a function of the number of pulleys that make up the arrangement. So, for example, a block and tackle with three pulleys would have a mechanical advantage of three.
Wheel and Axle
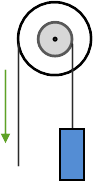
A wheel and axle uses two different diameter wheels mounted to a connecting axle. Force is applied to the larger wheel and large movements of this wheel result in small movements in the smaller wheel. Because a larger movement distance is being translated to a smaller distance, force is increased with a mechanical advantage equal to the ratio of the diameters of the wheels. An example of a wheel and axle is the steering wheel of a car.
Screw
A screw is an inclined plane wrapped in ridges (threads) around a cylinder. The distance between these ridges defines the pitch of the screw and this distance is how far the screw advances when it is turned once. The mechanical advantage of a screw is its circumference divided by the pitch.
Gears 7 2 6
Gear Trains
Connected gears of different numbers of teeth are used together to change the rotational speed and torque of the input force. If the smaller gear drives the larger gear, the speed of rotation will be reduced and the torque will increase. If the larger gear drives the smaller gear, the speed of rotation will increase and the torque will be reduced.
Gear Ratio
The mechanical advantage (amount of change in speed or torque) of connected gears is proportional to the number of teeth each gear has. Called gear ratio, it's the ratio of the number of teeth on the larger gear to the number of teeth on the smaller gear. For example, a gear with 12 teeth connected to a gear with 9 teeth would have a gear ratio of 4:3.
Applications
General 7 10
Force Lines of Action
Collinear forces act along the same line of action, concurrent forces pass through a common point and coplanar forces act in a common plane.
Bridge Forms
The six basic bridge forms are beam, truss, arch, cantilever, cable, and suspension.
Modulus of Elasticity
The modulus of elasticity measures how much a material or structure will deflect under stress. Stretch modulus is longitudinal stretch (like stretching raw bread dough), shear modulus is longitudinal deflection (like the horizontal displacement of a stack of magzines when a heavy object is placed upon them), and bulk modulus is compression of volume (like the compression of a loaf of bread under a heavy can at the bottom of a grocery bag).
Ceramics
Ceramics are mixtures of metallic and nonmetallic elements that withstand exteme thermal, chemical, and pressure environments. They have a high melting point, low corrosive action, and are chemically stable. Examples include rock, sand, clay, glass, brick, and porcelain.
Specific Gravity
Specific gravity is the ratio of the density of equal volumes of a substance and water and is measured by a hyrdometer.
Loads 6 7
Building Loads
Dead load is the weight of the building and materials, live load is additional weight due to occupancy or use, snow load is the weight of accumulated snow on a structure and wind load is the force of wind pressures against structure surfaces.
Structural Loads
A concentrated load acts on a relatively small area of a structure, a static uniformly distributed load doesn't create specific stress points or vary with time, a dynamic load varies with time or affects a structure that experiences a high degree of movement, an impact load is sudden and for a relatively short duration and a non-uniformly distributed load creates different stresses at different locations on a structure.